問：
　検定を行う場合，ケース数が大きければどのようなわずかの差であっても帰無仮説が棄却されることがあります。 逆に，ケース数が小さい場合にはどんなに差があっても帰無仮説は採択されてしまうことがあります。

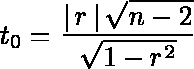
　例えば，相関係数の検定（母相関係数=0）を考えてみましょう。

　　　　帰無仮説 H0:「母相関係数ρ＝0」相関関係はない。
　　　　対立仮説 H1:「母相関係数ρ≠0」。
　　　　両側検定を行う。

　検定に用いられる式は，相関係数を r ，ケース数を n としたとき，以下のようになります。

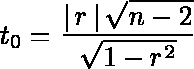equation

　この式を見れば明らかなように，ケース数が大きいほど，また，標本相関係数が大きいほど t0 の値は大きくなります。以下にいくつかの仮想例について検定を行った結果を示します。 

　　ケース数　標本相関係数   　t0    有意確率（P 値）  母相関係数の95%信頼区間
　　　　10        0.1　　   0.284268    0.7834244        　[-0.565，0.686]
　　　　50        0.1       0.696311    0.4895926        　[-0.183，0.368]
　　　 100        0.1       0.994937    0.3222174        　[-0.098，0.291]
　　　 250        0.1       1.582735    0.1147563        　[-0.024，0.221]
　　　 500        0.1       2.242834    0.0253466 * 　     [ 0.012，0.186]
　　　1000        0.1       3.175029    0.0015441 **     　[ 0.038，0.161]
　　　  10        0.3       0.889499    0.3996915   　     [-0.406，0.782]
　　　  10        0.5       1.632993    0.1411133        　[-0.189，0.859]
　　　  10        0.7       2.772413    0.0242063 * 　     [ 0.126，0.923]
　　　  10        0.9       5.839971    0.0003872 **     　[ 0.624，0.976]
　しかし，母相関係数=0の検定結果と，両者の相関が実質的に意味があるかどうかは無関係です。相関係数の解釈は以下のように行います。

　　  　相関係数の絶対値　　     解釈
            0.0〜0.2             ほとんど相関関係がない
            0.2〜0.4             やや相関関係がある
            0.4〜0.7             かなり相関関係がある
            0.7〜1.0             強い相関関係がある

　標本相関係数の2乗は一方の変数が他方をどれくらい説明できるかを表わすので，標本相関係数が 0.1 とは，わずか 1% しか説明できないことを表わします。にもかかわらず，ケース数が 1000 にもなると統計学的には「有意な相関がある」という検定結果が得られます。逆に，ケース数が 10 の場合には標本相関係数が 0.5 の場合（25%説明できる）でも，統計学的には「有意な相関があるとはいえない」ことになります。25% しか説明できないとはいうものの，読者は自分の持っているデータで相関係数が 0.5 以上になるのはどれくらいあるかみてみればよい。標本相関係数が 0.5 というのは，実際上は相当意味のある数値です。ちなみに，母相関係数の信頼区間は [-0.189，0.859] であるから，もしかしたらもう少しケース数を集めればもっと標本相関係数が大きくなることもあり得ます（当然，同じか，さらに小さな値の標本相関係数が得られるかもしれませんが）。

　平均値の差についても同じようなことがいえます。例えば，二つの群の体重の平均値の差が 0.1kg のときでも，「統計学的には有意差あり」ということになることもありますが，0.1kg の差は「実質的に何の意味も持たない」ということです。

　得られた知見に関する検定結果と実質的な意味の関係は以下のように 4 通りあります。得られた知見に意味がある場合にのみ，使用したケース数で仮説が妥当であるかどうかについて検定するのです（まず検定するという態度は誤りです）。逆に，実質的な意味があるのに検定結果が有意でないという状況は，ケース数が少ない場合や，測定精度が悪い（実験デザインが悪い）場合に生じます。データをよく吟味して，調査・研究を継続するのが妥当な対処法です。

実質的な意味 検定結果 取るべき行動
意味がある 有意である 得られた知見を採用する。
意味がある 有意でない ケース数を増やす。測定（調査）精度を高める。
意味がない 有意である 得られた知見は捨てる（そもそも検定などは不要である）。
意味がない 有意でない 得られた知見は捨てる（そもそも検定などは不要である）。

Last modified: May 15, 2002

・ 直前のページへ戻る　　・ E-mail to Shigenobu AOKI