全体としては無相関であるデータを，一方の変数で層別化してそれそれの変数の平均値をとった場合，計算された平均値の相関を計算すると大きな相関係数が計算されることがあるが，それは意味があることなのか，，，，という質問に対する答え。 
sim <- function(rep, n)
{
	result <- numeric(rep)
	for (i in 1:rep) {
		x <- rnorm(n)
		y <- rnorm(n)
		g <- ifelse(x  < -1.5, 1, ifelse(x  < -0.5, 2, ifelse(x  < 0.5, 3, ifelse(x  < 1.5, 4, 5))))
		xx <- tapply(x, g, mean)
		yy <- tapply(y, g, mean)
		result[i] <- cor(xx, yy)
	}
	result
}
hist(sim(1000, 300))
のような R プログラムを書いてシミュレーションしてみました。 このプログラムは，「相関のない正規変数を300組発生させ，片方の変数を -1.5, -0.5, 0.5 1.5 で層別し，それぞれの層ごとに平均値を求め，もう一方の変数も層ごとに平均値を求め，各層の5組の平均値についてピアソンの相関係数を求める」というものです。その相関係数の分布は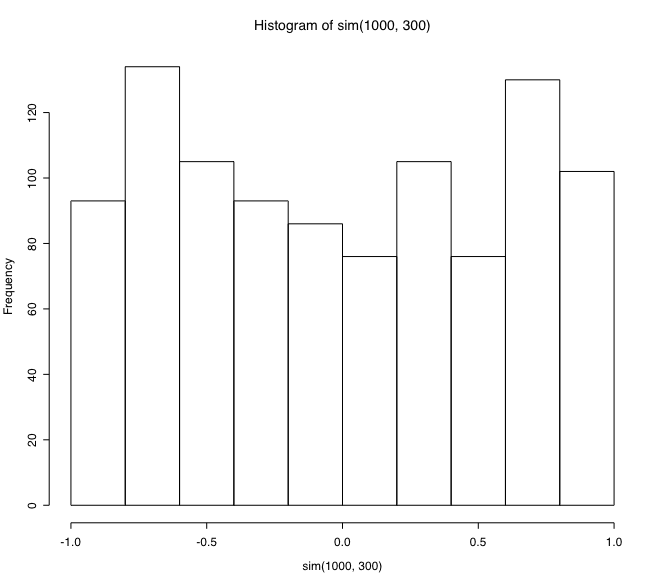
hist
のようになりました。実に幅広い相関係数が計算されることがわかります。
全体として無相関なデータから，層別の平均値をとって，その平均値間の相関を取ると，なぜ相関の高いケースが生じるかは
scat
のようなことがあるからです。
黒丸がもとのデータ，赤丸は横軸の5区分ごとの平均値を表すものです。
この図の時の，赤丸が表す5つのデータ点の相関係数は -0.9（！！！） 以上でした。
この例一つをとっても，先に述べたような手順で計算される相関係数は，たまたま生じる，取るに足らない傾向をとらえているにすぎないものだということがよくわかります。

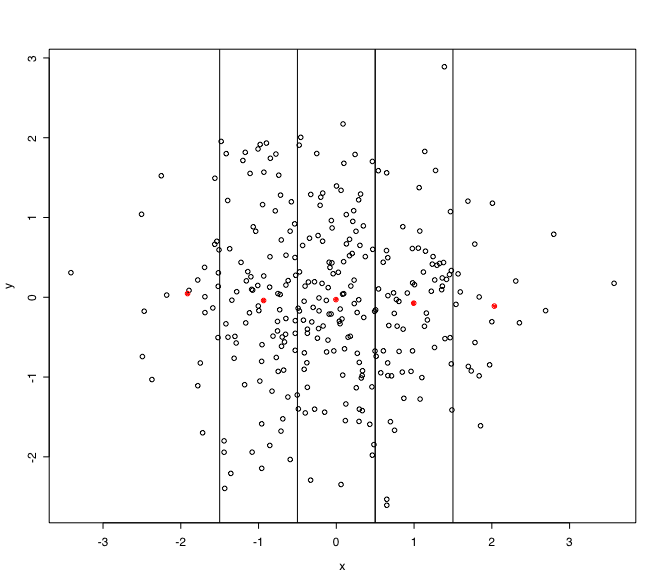
実際のデータ解析においても，全体のデータの散布図と，層別の平均値のプロットを描いて眺めてみると，層別の平均値間の相関係数が高くても，それは何の意味も持っていないと言うことがよく理解できるでしょう。