重回帰分析を行う

使用するデータセット

　dataset4.dat　データセットのダウンロード　注：ダウンロードの方法

　このデータセットは，5 変数 50 ケースからなるデータである。
　1 行目は変数名で，5 つの変数をそれぞれ，X1，X2，X3，X4，Y と名付けている。
　X1，X2，X3，X4 の変数は，../calculator/gendat2.html
により，表 1 に示す相関関係を持つように作られたものである。
表 1　各変数間の相関係数行列

X1        1.00000
X2        0.95000  1.00000
X3        0.30000  0.40000  1.00000
X4        0.20000  0.35000  0.20000  1.00000
               X1       X2       X3       X4
　また，変数 Y は，Y = 0.5*X1 + 1.4*X2 -2.3*X3 + 5.3*X4 + 誤差として生成したものである。

分析によって明らかになること

  1. X1，X2，X3，X4 の相関関係は，指定したとおり（表 1）のようになっている。
  2. 変数 X1 と変数 Y の相関係数は 0.36339，変数 X2 と変数 Y の相関係数は 0.45361 のように後者の方が大きいが，強い相関といえるほどではない。
  3. 変数 X1，X2 に対する偏回帰係数は理論的なものとはかけ離れたものになってしまう。変数 X3，X4 に対する偏回帰係数はほぼ理論的な値に近い。
  4. 変数 X1 は，変数 X2 より Y との相関は高くない（ほぼ等しい）にも関わらず，X1 の偏回帰係数は X2 の偏回帰係数の 4 倍程もある。これは，多重共線性の存在を疑わせる（事実，X1 と X2 のトレランスは低い）。

分析プロシージャの指定

　Black-Box の中の，「重回帰分析」を指定する

分析オプションの指定

　「variables=1-4/dependent-variable=5」を指定する。すなわち，1 〜 4 番目の変数（X1,X2,X3,X4）を独立変数，5 番目の変数（Y）を従属変数として重回帰分析を行う。

分析結果

重回帰分析　　　Thu Jul 23 11:50:48 1998


データセット名: dataset4.dat
ケース数:       50
変数の個数:     5
有効ケース数：  50
従属変数：　　  Y


                     平均値           不偏分散           標準偏差
Y              2.8257264000       36.300301839       6.0249731816
X1        -1.9999999997e-07       1.0204074721       1.0101522024
X2         1.9999999998e-07       1.0204074206       1.0101521769
X3         1.9999999998e-07       1.0204074859       1.0101522093
X4         1.3877787808e-17       1.0204085624       1.0101527421


***** 相関係数行列 *****

Y         1.00000
X1        0.36339  1.00000
X2        0.45361  0.95000  1.00000
X3       -0.07966  0.30000  0.40000  1.00000
X4        0.89519  0.20000  0.35000  0.20000  1.00000
                Y       X1       X2       X3       X4
　X1 と X2 の相関係数が非常に大きい。
　Y と X1，Y と X2 の相関係数の大きさは同じ程度である。 

従属変数: Y
独立変数:
     X1        X2        X3        X4


***** 重回帰式 *****

             偏回帰係数       標準誤差         ｔ値       Ｐ値   標準化偏回帰係数
X1             1.437909      0.7870787    1.8268935    0.07435      0.2410811
X2            0.3014271      0.8492725    0.3549239    0.72430     0.05053753
X3            -2.100299      0.2396473    8.7641262    0.00000     -0.3521380
X4             5.366253      0.2525180   21.2509731    0.00000      0.8997112
定数項         2.825727      0.2104203   13.4289687    0.00000
                                              ｔ値の自由度: 45
　X1 と X2 に対する偏回帰係数の値は理論的なもの（Y = 0.5*X1 + 1.4*X2 -2.3*X3 + 5.3*X4 + 誤差）とは大きく異なる。 
              トレランス     分散拡大係数
*X1           0.07147251         13.99139
*X2           0.06138769         16.28991
 X3            0.7709572         1.297089
 X4            0.6943688         1.440157

  警告: [*] が付いている変数は多重共線性の原因になっているかもしれません。
　X1 と X2 のトレランスが非常に低い。多重共線性が存在することを表している。 

***** 分散分析表 *****

要因            平方和    自由度       平均平方           Ｆ値      Ｐ値
回帰          1679.092         4       419.7731       189.6136    0.00000
残差          99.62254        45       2.213834
全体          1778.715        49


重相関係数:                     0.97159
決定係数（重相関係数の二乗）:   0.94399
自由度調整済み重相関係数の二乗: 0.93901
　多重共線性の存在にも関わらず，「予測」という意味ではうまくいっている。 

***** 従属変数の観察値，予測値および標準化残差 *****

ケース         観察値         予測値           残差     標準化残差
     1       7.564370       8.194869     -0.6304991     -0.4574171
     2      -1.543280      0.5436742      -2.086954      -1.534843
     3      -1.927160       1.144739      -3.071899      -2.239373
     4       6.161750       4.904043       1.257707      0.8651420
     5      -5.544570      -6.159107      0.6145370      0.4384877
     6       3.318390       3.538671     -0.2202810     -0.1541730
     7      0.2020100       2.084277      -1.882267      -1.328011
     8       5.647760       4.075862       1.571898       1.089108
     9       3.271970       5.679764      -2.407794      -1.650139
    10       1.096520       2.281021      -1.184501     -0.8082908
    11       6.554310       4.757478       1.796832       1.259547
    12      -4.176690      -3.564859     -0.6118313     -0.4243961
    13       12.30735       13.77904      -1.471687      -1.058350
    14       2.008980       2.619280     -0.6102996     -0.4213461
    15       2.190970       1.872992      0.3179778      0.2170358
    16      -5.833490      -5.879693     0.04620257     0.03295815
    17       15.30856       13.96208       1.346478      0.9936504
    18       4.119860       3.376675      0.7431854      0.5067373
    19       3.925170       3.925944  -0.0007739403  -0.0005506149
    20       13.87460       13.79525     0.07935053     0.05826873
    21       3.882000       3.621157      0.2608430      0.1865109
    22      0.7884400      0.9796844     -0.1912444     -0.1309081
    23      -13.07343      -14.00026      0.9268325      0.7127861
    24       11.67901       9.676212       2.002798       1.384191
    25       4.981690       3.152877       1.828813       1.253335
    26      -1.003410      -2.857383       1.853973       1.288673
    27       7.563400       7.887087     -0.3236868     -0.2290932
    28       1.171190      0.1581504       1.013040      0.6935883
    29       6.353930       6.295012     0.05891756     0.04074628
    30       4.683860       3.458838       1.225022      0.8352115
    31      -4.224920      -2.649384      -1.575536      -1.109855
    32       9.498160       9.817994     -0.3198340     -0.2308663
    33       5.839920       5.222794      0.6171260      0.4533808
    34     -0.6428900       1.675641      -2.318531      -1.576996
    35      -5.054650      -5.852777      0.7981272      0.5677525
    36      0.2862100      -1.218111       1.504321       1.040496
    37       10.19746       11.16406     -0.9666022     -0.6901640
    38      -3.190940      -4.434079       1.243139      0.9086439
    39      -5.891580      -3.591877      -2.299703      -1.606627
    40       9.678050       6.950016       2.728034       2.024272
    41       5.278070       7.109839      -1.831769      -1.369854
    42       3.509110       4.806999      -1.297889     -0.9081194
    43       4.286720       5.015423     -0.7287028     -0.5087180
    44       10.00550       8.382044       1.623456       1.200726
    45       9.867990       10.95565      -1.087657     -0.7714314
    46       1.069450      0.3437755      0.7256745      0.5253381
    47      -7.501600      -5.034111      -2.467489      -1.810677
    48       8.241260       6.557877       1.683383       1.178679
    49      -2.678950      -4.004726       1.325776      0.9653030
    50      -2.840110      -3.234097      0.3939871      0.2745766

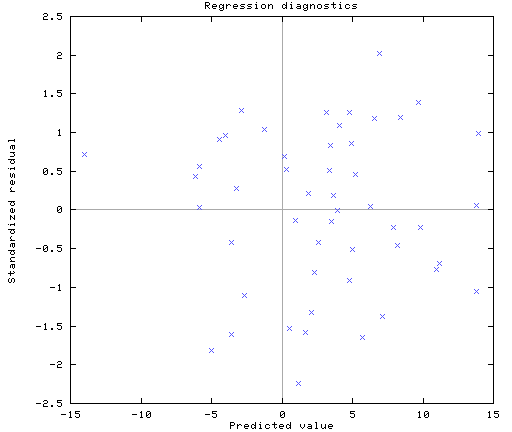
***** 回帰診断：予測値と標準化残差のプロット *****




予測値と標準化残差のプロット





***** 予測値と観察値のプロット *****




予測値と観察値のプロット
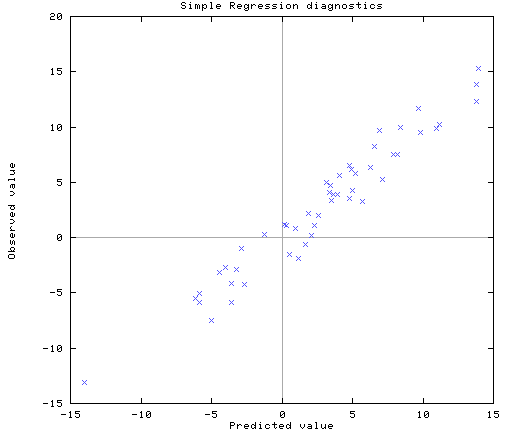　多重共線性の存在にも関わらず，「予測」という意味ではうまくいっている。しかし，どの独立変数が従属変数に影響を及ぼしているかを考えるときに，偏回帰係数が与える情報だけを頼りにすると結論を誤る可能性が大きい。

演習

  1. X1 を除いて，X2，X3，X4 だけを使って Y を予測する重回帰分析を行い，結果を比較せよ。
  2. X2 を除いて，X1，X3，X4 だけを使って Y を予測する重回帰分析を行い，結果を比較せよ。
・ 直前のページへ戻る　　・ E-mail to Shigenobu AOKI

Made with Macintosh